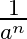\((8a+3b+2c+d):2\) oder \((8a\cdot 3b\cdot 2c\cdot d):2\)
Bei der Summe muss jeder Summand durch zwei geteilt werden, bei dem Produkt genügt es, einen Faktor durch zwei zu teilen (wenn das geht...)
\((8a+3b+2c+d):2=4a+\frac32 b + c +\frac12d\) bzw.
\((8a\cdot 3b\cdot 2c\cdot d):2 = 4a \cdot 3b\cdot 2c \cdot d = 24abcd\)
- Grenzverhalten im Unendlichen (Arme und höchste Potenz)
- Verhalten nahe 0 (kleinste Potenz - aussehen im Bereich der y-Achse)
- y-Achsenabschnitt (siehe auch Verhalten Nahe 0)
- Manchmal auch Nullstellen (Linearfaktoren)
- ggf. auch Symmetrie prüfen (ungerade Exponenten - punktsymm...)
... kürzen nur die Dummen
... wurzeln nur die Dummen
oder die ganz Schlauen
Nur bei Geraden: \(f(x)=y=m\cdot x+b\)
Diese Funktionen haben überall die gleiche Steigung -
Bei anderen Funktionen von Koeffizienten, Vorfaktoren oder auch Streckungs- bzw. Stauchungsfaktoren sprechen
durch die Punkte
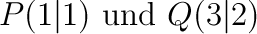
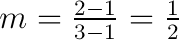
einer der Faktoren Null ist.
... sie nur gerade Potenzen von x enthält, z.B.
\(f(x) = x^4 + 2 \cdot x^0 - \frac{3}{x^2} = x^4 +2-3x^{-2}\)
... sie nur ungerade Potenzen von x enthält, z.B.
\(f(x) = x^7 + 2 \cdot x^1 - \frac{3}{x} = x^7 +2x-3x^{-1}\)
... der Abstand der Funktionswerte von der x-Achse (\(|f(x)|\)) für sehr große x-Werte immer kleiner wird (auch für sehr kleine - im Sinne von -10000), z.B. \(\frac{1}{x}\)
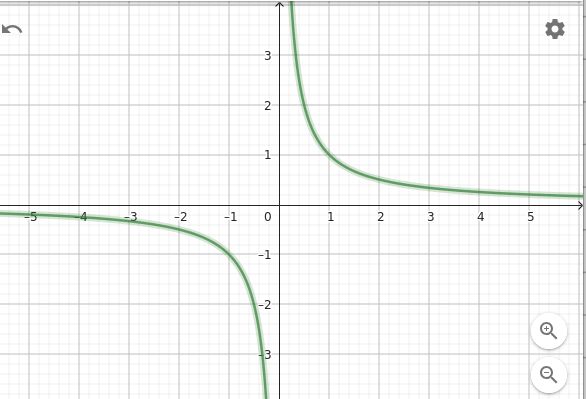
geht man im Bild entlang der x-Achse immer weiter nach links oder rechts, so nähert sich der Funktionswert (grün) der x-Achse an.
Erst strecken und spiegeln, dann verschieben
Sonst würde die Verschiebung auch nochmal gestreckt oder gespiegelt...
... mit dem Kehrwert malnimmt
Beispiel: \(\begin{array}{rl} \frac12x^2-x-4&=0 \qquad|:\frac12 \Leftrightarrow\cdot 2 \\ x^2-2x-8&=0 \end{array}\)
Klammer vor Potenz vor Punkt vor Strich und dann von links nach rechts
Wenn der Betrag des Streckungs- bzw. Stauchungsfaktors a kleiner als 1 ist (\(|a|<1\) ), ist sie gestaucht, ansonsten gestreckt.
Sie sind parallel, wenn sie sich nicht schneiden und somit die gleiche Steigung haben.
Die Steigung m ist also bei beiden geraden gleich. Ist der y-Achsenabschnitt nicht verschieden, so sind die geraden sogar identisch (oh Wunder ;-) )
Es ist das Äquivalenzzeichen und bedeutet, dass die Gleichungen vor und nach dem Zeichen die gleiche Lösungsmenge haben, d.h. gleichwertig (äquivalent) sind.
Es bedeutet "ist Element von"
\(n \in \mathbb{N}\) - heißt, dass n Element der natürlichen Zahlen ist.
Er bestimmt, wie weit die Zahl vom Ursprung weg ist.
|5| = 5 und |-5| = 5
Er ist immer eine nichtnegative Zahl also größer oder gleich 0
Es bedeutet "ohne" - also C enthält alle Elemente aus A ohne die aus B
Es bedeutet, dass der Funktionswert immer größer wird (gegen unendlich strebt), wenn x immer größer wird (gegen plus unendlich strebt)
Bildlich gesprochen: der rechte "Arm" der Funktion geht nach oben, sie "verschwindet" im ersten Quadranten (so wie \(x^2\))
Lies: Limes von f von x für x gegen plus unendlich strebt (läuft gegen) unendlich
Das steht für oder: \(x=1\vee x=2\)
Lies x gleich 1 oder x gleich 2
Das steht für und: \(x>1\wedge x<2\)
Lies x größer 1 und x kleiner 2,
also \(1<x<2\) oder \(x\in(1,2)\)
Ein negativer Faktor sorgt für eine Spiegelung an der x-Achse
Wenn der Betrag größer 1 ist, wird die Funktion zudem noch gestreckt....
Eine ungerade Funktion
Hinweis: ähnlich wie bei "Minus mal Minus ergibt plus"
Eine gerade Funktion
Hinweis: Ähnlich wie bei "Minus mal Minus gibt Plus"
Bei einer ganzrationalen Funktion gibt es zu jeder Nullstelle einen entsprechenden Linearfaktor
z.B. gehört zur Nullstelle \(x=-2\) der Linearfaktor \((x+2)\)
\(x^0 = 1 \text{ für alle }x \ne 0\)
\(0^0\) ist nicht definiert
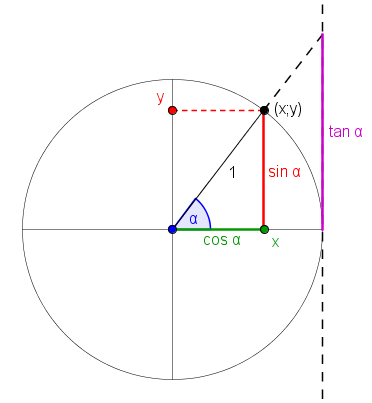
Beim Bogenmaß wird der Winkel nicht in Grad gemessen, sondern man gibt die Länge des Bogens am Einheitskreis an.
Das heißt 360° ≙ 2π (dem Umfang des Einheitskreises). Dementsprechend 180° ≙ π, 90° ≙ π/2, usw.
Das große Delta wird oft für eine Differenz verwendet
\(\Delta y = y_2-y_1\)
Eine Stelle ist nur die x-Koordinate, ein Punkt hat sowohl die x- als auch die y-Koordinate.
Bei einer ungeraden Funktion sind alle(!) Exponenten ungerade und die Funktion ist somit punktsymmetrisch zum Ursprung.
Bei ungeradem Grad ist nur der größte Exponent (der Grad) ungerade.
Die Amplitude ist die maximale Auslenkung aus der Ruhelage (oder auch Nulllage).
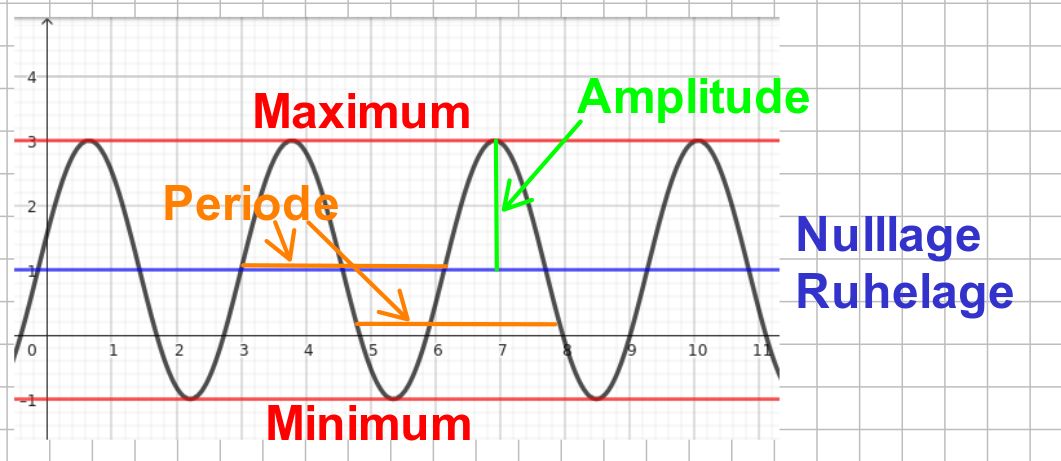
Man kann sie auch als halbem Abstand zwischen Maximum und Minimum definieren.
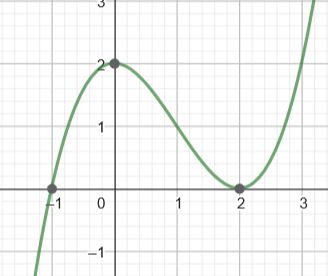
Der Graph der Funktion berührt die x-Achse an dieser Stelle nur, er schneidet sie nicht. Der Linearfaktor ist doppelt in der Funktionsgleichung enthalten.
\(f(x)=\frac12(x+1)\cdot (x-2)^2\)
Die Menge aller Zahlen, die in eine Funktion eingesetzt werden können.
f(x) = 1/(x-1) - hier dürfen alle Werte außer 1 eingesetzt werden
Beispiel: Wenn es regnet ist die Strasse nass
Die Kontraposition ist Wenn nicht B dann nicht A \((\neg B\Rightarrow\neg A)\)
Wenn die Strasse nicht nass ist, regnet es auch nicht
Achtung: Nicht wenn es nicht regnet ist die Strasse nicht nass - das kann Falsch sein!
Der kleinste Abstand zweier Stellen der Funktion bei denen sich die Funktion wiederholt

(gleicher Funktionswert reicht nicht)
Die Menge aller Zahlen, die eine Funktion beim Einsetzen aller Werte der Definitionsmenge annehmen kann.
z.B. bei einer Parabel, die nach oben geöffnet ist, werden nur die Werte oberhalb des Scheitelpunktes (inklusive) angenommen:
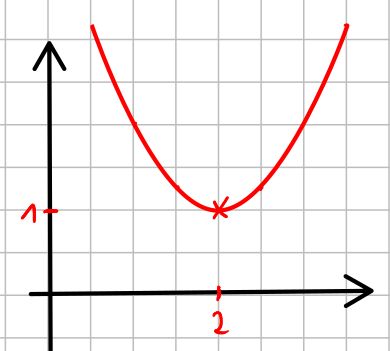 in diesem Beispielt besteht die Wertemenge also aus allen Zahlen größer oder gleich 1:
in diesem Beispielt besteht die Wertemenge also aus allen Zahlen größer oder gleich 1: Ein Beweis ist ein logisch aufgebautes Argument, das zeigt, dass eine Aussage wahr ist.
Bestandteile:
- Aussage: Der zu beweisende Sachverhalt. Sie besteht aus
Voraussetzungen: Gegebene oder als wahr angenommene Bedingungen.
Behauptung: Was gezeigt werden soll. - Logik: Nutzung logischer Regeln und Schlussfolgerungen, um die Behauptung aus den Voraussetzungen herzuleiten.
Ziel: Gewissheit über die Wahrheit der Aussage.
Ein Intervall ist ein „Zeitraum“ also eine Menge an Zahlen, die durch eine Start- und Endzahl begrenzt sind. Z.b.:
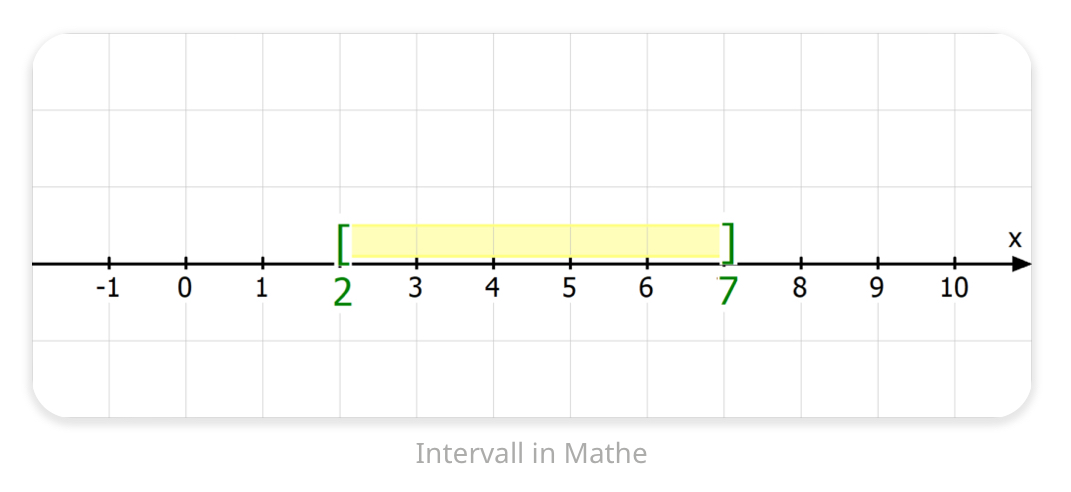
Achtung \([3,5)\) - bedeutet 3 inklusive und 5 exklusive - oder auch \([3; 5[ = \lbrace x \in \mathbb{R} | 3 \le x < 5 \rbrace \)
Ein Koeffizient ist eine Vorzahl, z.B. vor der Variable “x”
Beispiel: -0,25·x3 – 0,5·x2 + 1,25·x + 1,5
Ein Faktor, der Form \((x+c)\) mit einer reellen Zahl \(c \in \mathbb{R}\)
Jedem x wird höchstens ein y zugeordnet.
Eine Normale ist eine Senkrechte zur Funktion, sie liegt somit um 90° gedreht zur Tangente. Ihre Steigung erhält man als negativen Kehrwert der Tangentensteigung:
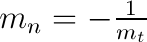
- Der Graph schneidet die x-Achse
- Stelle x mit f(x) = 0, d.h. eine Stelle x an der der Funktionswert gleich 0 ist
Das ist eine Gerade, die die Parabel nicht schneidet.
Eine Gerade, die an einem Objekt vorbei läuft.
Der Funktionsterm hat die Form \(f(x)=a\cdot x^n\) ,
Der Exponent n kann dabei aus den reellen Zahlen sein, aber insbesondere auch aus den ganzen Zahlen, also auch negativ.
Eine Gerade, die die Parabel an zwei Stellen berührt.
Eine Gerade, die ein Objekt schneidet (secare - schneiden)

Eine Gerade, die die Parabel in einem Punkt berührt.
Eine Gerade (unendlich) die ein Objekt berührt (nicht schneidet)

Eine Funktion die Achsensymmetrisch zur y-Achse ist (z.B. cos(x) oder x²)
Eine Funktion die punktsymmetrisch zum Ursprung ist (z.B. sin(x) oder x³)
Die Nullstellen (und den Streckungsfaktor)
\(f(x) = a \cdot (x-r)\cdot (x-s)\)
Man benötigt mehrere Gleichungen - mindestens so viele wie es Unbekannte gibt.
(Lineares) Gleichungssystem (L)GS
Einsetzungsverfahren, Aditionsverfahren, ...
Das bedeutet "soll gleich sein", z.B. wenn man einen Punkt in eine Funktionsgleichung einsetzt um zu prüfen, ob er drauf liegt.
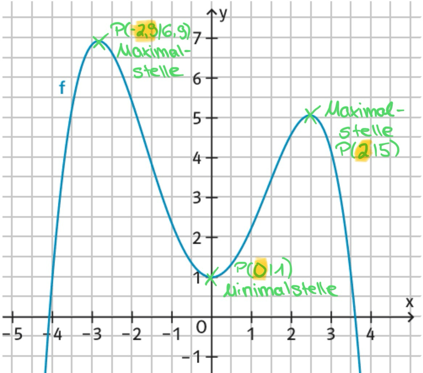
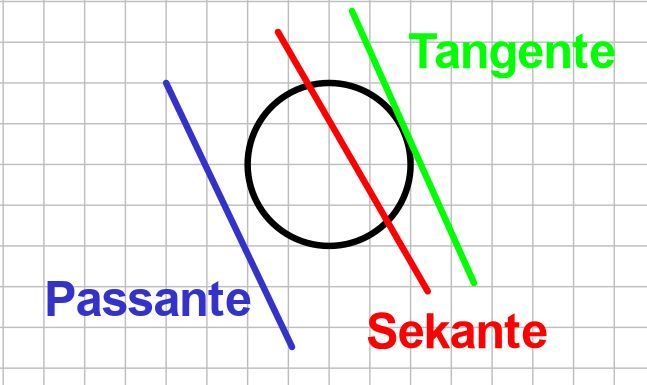
Extremstellen sind die x-Werte der Extrempunkte, sie werden als Minimalstelle und Maximalstelle bezeichnet.
An Extrempunkten wechselt der Graph die Steigung. 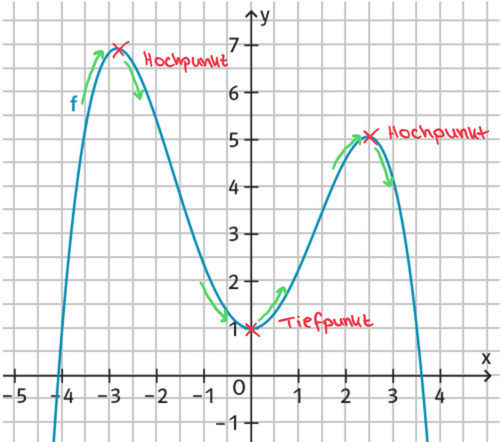

Eine Hochpunkt, ist der Wechsel von positiver zu negativer Steigung in dem Graphen und der Tiefpunkt somit der Wechsel von negativer zu positiver Steigung im Graphen.
- Schnittpunkte mit den Achsen (Nullstellen, Schnittpunkt mit der y-Achse)
- Extrempunkte (Hochpunkt, Tiefpunkt)
- Maximum / Minimum
- Wendepunkte
ganzrationale Funktionen sind Summen aus Potenzfunktionen \[f(x)=a_n x^n + a_{n-1}x^{n-1} + … + a_1 x + a_0\]Diese Funktionen enthalten Koeffizienten \(a_i , i = 0,1, \dots\) , diese sind irgendwelche reellen Zahlen. Die Exponenten sind natürliche Zahlen.
- Vorwärtsarbeiten:
- Ausgangspunkt (z. B. eine Gleichung) schrittweise zielorientiert Richtung Lösung umformen
- Fokus auf korrekten Rechenregeln bei jeder Umformung.
- Rückwärtsarbeiten:
- Vom Ziel (z. B. gewünschte Lösung oder Form) ausgehen und überlegen, welche Schritte zur Ausgangsgleichung führen könnten.
- Hilft, die Lösungsidee oder angemessene Rechenschritte zu entwickeln.
Hinweis: Beide Techniken werden oft kombiniert, um komplexe Gleichungen effizient zu lösen. Und helfen auch bei Beweisen
Die "Geschwindigkeit" mit der sich eine Größe ändert.
Ist sie positiv so nimmt die Größe zu, je größer um so schneller.
Wenn in einer Funktion das x unter einem Bruchstrich auftaucht, könnte die Regel "Man darf nicht durch 0 teilen" verletzt werden.
Wurzeln, denn bei Wurzeln darf nichts negatives unter der Wurzel stehen
Sie hat die Nullstellen 2 und -2, da man die Funktion aufgrund der dritten binomischen Formel schreiben kann als:
\(f(x) = (x-2)(x+2)(x-2)(x+2)=(x-2)^2(x+2)^2\)
Punktsymmetrie zum Ursprung, denn
z.B. der Funktionswert \(f(-5)\) an der Stelle -5 entspricht dem negativen Funktionswert an der Stelle 5: \(-f(5)\)
Achsensymmetrie zur y-Achse, denn
z.B. der Funktionswert \(f(-5)\) an der Stelle -5 entspricht dem Funktionswert \(f(5) \)an der Stelle 5
- Wenn die Linearfaktoren vorliegen, kann man die Nullstellen ablesen \(f(x)=3(x-2)²\cdot (x+3)\).
- Ansonsten kann man durch Ausklammern den Grad verringern. \(f(x)=3x^3-x = x(3x^2-1)\)
- Man verwendet den Nullproduktsatz: "Ein Produkt ist Null, wenn einer der Faktoren null ist"\(x(3x^2-1)=0 \Leftrightarrow x=0 \vee 3x^2-1=0\)
- Bei einer ganzrationalen Funktion vom Grad 2: pq-Formel oder ähnliches.
Fortgeschritten: Nullstelle Raten - Polynomdivision \(x^3-2x^2+1\) hat die Nullstelle \(x=1\). Man kann also durch den Linearfaktor \((x-1) \) teilen \(x^3-2x^2+1=(x-1)\cdot (x^2-x-1)\). Nun kann man den Nullproduktsatz mit pq-Formel anwenden: \(x=1\vee x=\frac12\pm\sqrt{\frac14+1}\)
Der Differenzenquotient (Höhenunterschied durch Horizontalunterschied) bestimmt die Steigung einer Sekante. Läßt man nun die beiden Punkte der Sekante die auf der Funktion liegen immer näher zusammenrücken, so wird die Sekante zur Tangenten. Die Steigung der Sekanten nähert sich also immer mehr der Steigung der Tangenten an.
dreht sich das Ungleichheitszeichen um.
(aus größer wird kleiner und umgekehrt)
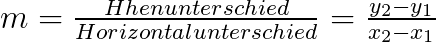
Der Parameter kann gut abgelesen werden an der Selle wo die Sinusfunktion zum ersten mal die Nulllage steigend schneidet
Der Parameter d kann gut an dem Abstand der Nulllage/Ruhelage von der x-Achse abgelesen werden.

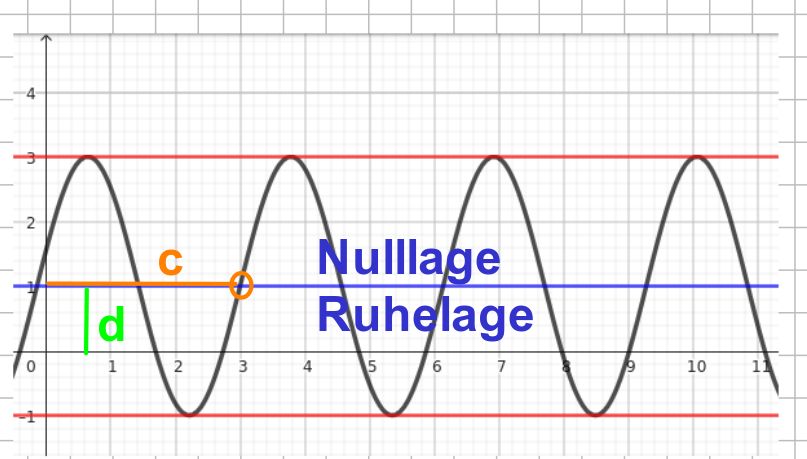
Es gilt \(m=\tan(\alpha)\). Mit \(m\) ist die Steigung der Geraden und \(\alpha\) der Steigungswinkel
Man geht vom Scheitelpunkt aus einen Schritt zur Seite und schaut wie viele Schritte man nach oben gehen muss, dies entspricht dem Streckungsfaktor.
Man kann auch 2,3,... Schritte zur Seite gehen und vergleicht dann die Schritte die man nach oben/unten gehen muss, mit den Schritten bei der Normalparabel (4, 9, ...).
Bsp: Wenn man zwei Schritte vom Scheitelpunkt zur Seite geht, müsste man bei der Normalparabel 4 nach oben gehen.
Wenn man im Bild aber nur einen Schritt nach oben gehen muss, dann ist der Stauchungsfaktor 1/4. Denn die "normalen" 4 müssen mit 1/4 multipliziert werden um auf 1 zu kommen.
Es gilt \(p=\frac{2\cdot \pi}{|b|}\)
Weil die Periode (Wiederholungslänge) der normalen Sinus-Funktion \(2\pi\) ist und der Faktor \(b\) zu einer Streckung in x-Richtung um den Faktor \(\frac{1}{b}\) führt - Das Vorzeichen von \(b\) spielt hier keine Rolle (Spiegelung an der y-Achse)
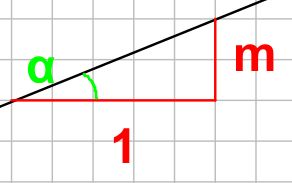
Man berechnet den Höhenunterschied durch den Horizontalunterschied
\(m = \frac{y_2-y_1}{x_2-x_1}=\frac{\Delta y}{\Delta x}=\frac{\text{Höhenunterschied}}{\text{Horizontalunterschied}}\)
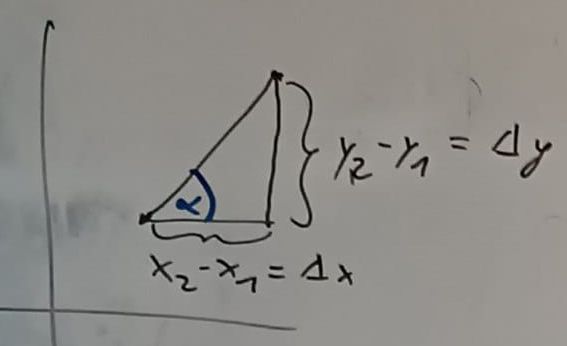
Mit dem Steigungsdreick. Die Steigung m ist dann der Höhenunterschied durch den Horizontalunterschied.

In dem man den y-Achsenabschnitt b und die Steigung m abliest.
Oder man ermittelt nur die Steigung aus zwei Punkten und berechnet den y-Achsenabschnitt durch einsetzen.
Steigung berechnen (Steigungsdreieck), dann einen Punkt in die Gleichung einsezten und den y-Achsenabschnitt b berechnen.
Entweder kann man in einem Rechendokument (auch Scratchpad) die Funktion zeros nutzen
zeros(f(x),x) - dies geht auch über das Menü-> 3(Algebra)-> NullstellenDurch das Rundungszeichen \(\approx \)
Den Grad erkennt man an dem größten Exponenten aller Potenzen von x.
Beispiel: -0,25x3 – 0,5x2 + 1,25x + 1,5 -> Diese Funktion ist eine ganzrationale Funktion dritten Grades.
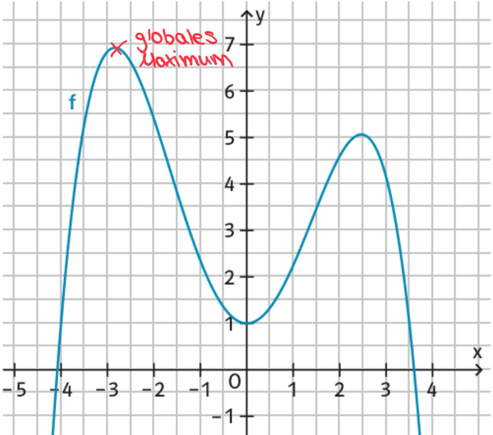
Nur wenn ein Tiefpunkt auch der niedrigste Punkt des gesamten Graphen ist, wird er globales Minimum genannt. Das Globale Maximum ist dann der höchste Punkt des gesamten Graphen.
Hinweis: Der Graph im Beispiel hat kein globales Minimum
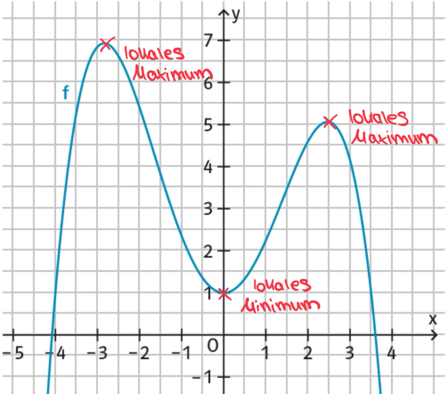
Wenn ein Tiefpunkt vorliegt, dann ist er in seiner Umgebung der tiefste Punkt und wird dann auch als lokales Minimum bezeichnet. Das ist beim lokalen Maximum genauso, wenn ein Hochpunkt in seiner Umgebung der höchste ist.
Hinweis: Eine Umgebung ist ein Intervall um die Stelle des Punktes, z.B. wenn die Stelle -3 ist , dann wäre ein Intervall [-3.5 , -2.5] eine Umgebung um die Stelle 3
Hinweis: Eine Umgebung ist ein Intervall um die Stelle des Punktes, z.B. wenn die Stelle -3 ist , dann wäre ein Intervall [-3.5 , -2.5] eine Umgebung um die Stelle 3
\(f(x)=ax^2 + bx + c\)
- Vorfaktor ausklammern - \(f(x) = a \cdot\left ( x^2 + \frac{b}{a} x + \frac{c}{a} \right )\)
- p identifizieren und mit \(\left( \frac{p}{2} \right )^2\) ergänzen - \(f(x) = a \cdot\left ( x^2 + \frac{b}{a} x + \left( \frac{b}{2a} \right)^2 - \left( \frac{b}{2a} \right)^2+ \frac{c}{a} \right )\)
- binomische Formel anwenden und ggf. Klammer auflösen
\(f(x) = a \cdot\left ( \left ( x + \frac{b}{2a} \right)^2 - \left( \frac{b}{2a} \right)^2+ \frac{c}{a} \right ) = a \cdot \left ( x + \frac{b}{2a} \right)^2 - \frac{b^2}{4a} + c\)
Jetzt hätte man sogar eine Formel für den Scheitelpunkt - man kann also direkt aus der Normalform den Scheitelpunkt ablesen: Die x-Koordinate des Scheitelpunktes ist einfach b/(2a)
Der Graph von f wird mit dem Faktor \(a\) (\(a\ne0)\) in y-Richtung ⬍ gestreckt
Für \(a<0 \) also negative \(a\) wird der Graph an der x-Achse gespiegelt ⬍
Der Graph von f wird mit dem Faktor \(\frac1b\) \((b\ne0)\) in x-Richtung ⬌ gestreckt. Also für \(b>1\) gestaucht!
Für \(b<0 \) also negative \(b\) wird der Graph an der y-Achse ⬌ gespiegelt
Der Graph von f wird um d Einheiten in y-Richtung ⬍ verschoben.
Der Graph von \(f\) wird um \(c\) Einheiten in x-Richtung ⬌ verschoben.
\(\mathbb{N}=\lbrace 1,2,3,\dots \rbrace\)- natürliche Zahlen

\(\mathbb{Z}=\lbrace \dots, -3,-2,-1,0,1,2,3,\dots \rbrace\)- ganze Zahlen
\(\mathbb{Q}=\left \lbrace \frac{p}{q} \middle | p\in \mathbb{Z} \text{ und } q \in \mathbb{N} \right \rbrace\)- rationale Zahlen
\(\mathbb{R}\)- reelle Zahlen
Gewinn ist Umsatz minus Kosten \(G(x) = U(x)-K(x)\)
\(m = \tan (\alpha)\)
Die Ableitung an einer Stelle ist die Steigung der Tangente an die Funktion an dieser Stelle.
\(U(x)=p\cdot x\), wobei \(p\) der Preis des Produktes ist und \(x\) die Stückzahl
Potenzen mit gleicher Basis werden multipliziert (dividiert) in dem man die Exponenten addiert (subtrahiert) und die Basis beibehält.
\(b^5 \cdot b^3 = b^8\) bzw. \(\frac{c^3}{c^7} = c^3 : c^7 = c^{3-7}=c^{-4}\)
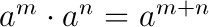
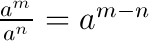
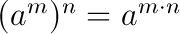
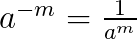

alle reellen Zahlen \(\mathbb{D} = \mathbb{R}\)

\(\lim_{h \to 0} \frac{f(x_0 + h) - f(x_0)}{h}\)
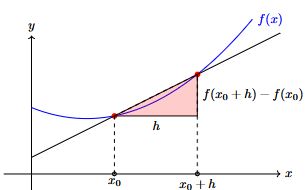
h wird immer kleiner
Ein Produkt (Ergebnis) ist immer dann Null, wenn mindestens ein Faktor, also ein „Part“ der Rechnung gleich Null ist.

alle reellen Zahlen >= 1
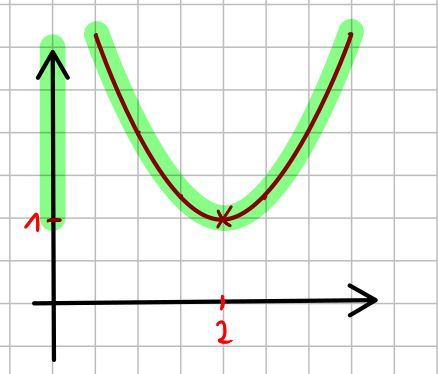
\(\mathbb{W} = \mathbb{R}^{\ge 1} = \lbrace x \in \mathbb{R} \mid x \ge 1 \rbrace\)
\(y=m\cdot (x-p_x)+p_y\) ist die Gerade durch den Punkt \(P(p_x|p_y)\) mit der Steigung \(m\)
Kann man sich so erklären, dass die Ursprungsgerade \(y=m\cdot x\) in den Punkt P verschoben wurde. \(p_x\) nach rechts und \(p_y\) nach oben.
\(f(x) = a\cdot (x-d)^2 + e\) hat den Scheitelpunkt \(S(d|e)\)
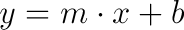
y = m · x + b
\((a+b)\cdot (a-b)=a^2-b^2\)
\(x_{1,2}=- \frac{p}{2}\pm \sqrt{\left (\frac{p}{2} \right )^2 - q}\)
f Strich von x ist die Ableitung der Funktion \(f\) an der Stelle x, also die Steigung der Tangente an die Funktion oder auch die Änderungsrate
- Alles auf eine Seite bringen (Andere Seite ist 0)
- Durch den Faktor vor \(x^2\) teilen
- p/q-Formel anwenden
Alternativ: Quadratische Ergänzung oder in einfachen Fällen Wurzel ziehen (PlusMinus nicht vergessen)
Es handelt sich um eine Darstellung in Linearfaktoren - hier kann man gut die Nullstellen ablesen. Diese liegen bei \(x=2\) und eine doppelte Nullstelle bei \(x=-3\)
\(\mathbb{D} = \mathbb{R} \setminus \lbrace 1 \rbrace = \lbrace x \in \mathbb{R} \mid x \ne 1 \rbrace\)
In dem man sie auf die andere Seite des Bruchstriches schreibt (Zähler <-> Nenner)
\(a^{-2}=\frac{1}{a^2}\)
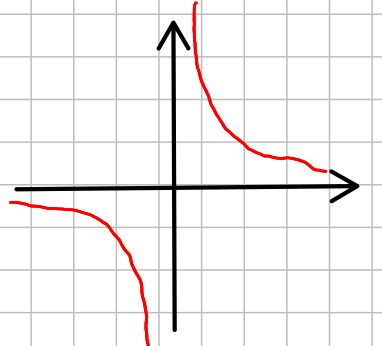 Wie eine Hyperbel. Sie nähert sich jeweils asymptotisch den Achsen und verläuft durch den ersten und dritten Quadranten des Kooridnatensystems.
Wie eine Hyperbel. Sie nähert sich jeweils asymptotisch den Achsen und verläuft durch den ersten und dritten Quadranten des Kooridnatensystems.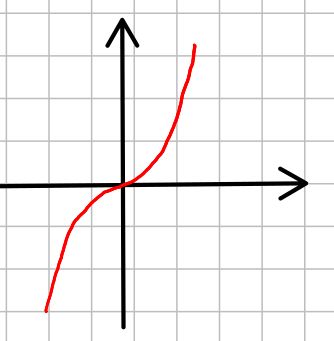 Wie eine „Skischanze“ von links unten kommend nach rechts oben verlaufend
Wie eine „Skischanze“ von links unten kommend nach rechts oben verlaufend
Es wäre eine gepunktete Funktion
Sie kann höchstens vier Nullstellen haben, da sie aus höchstens vier Linearfaktoren bestehen kann.
"Jedes mit Jedem", d.h.
jeder Summand der einen Klammer mit jedem Summand der anderen Klammer
\((a+b)\cdot (c+d) = a\cdot c + a\cdot d + b\cdot c + b\cdot d\)
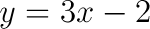
Man zeichnet zunächst den y-Achsenabschnitt -2 ein und dann geht man eine Einheit zur Seite und drei Einheiten nach oben (Steigung m=3).
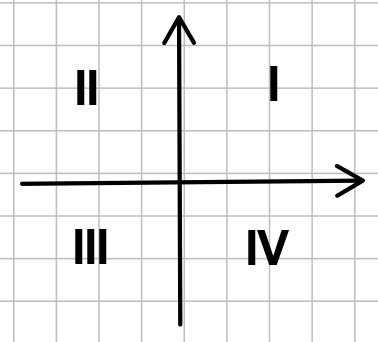 Der erste Quadrant ist der mit den beiden positiven Achsenteilen. Dann wird im mathematisch positiven Sinn (also gegen den Uhrzeigersinn) weitergezählt.
Der erste Quadrant ist der mit den beiden positiven Achsenteilen. Dann wird im mathematisch positiven Sinn (also gegen den Uhrzeigersinn) weitergezählt.Man schaut sich die kleinsten Potenzen an, z.B. bei \(f(x) = -x^4+3x-2\) ist der Verlauf nahe der y-Achse wie eine Gerade: \(y = 3x-2\)
Sie haben die gleiche Steigung
Das Produkt ihrer Steigungen ergibt -1.
Hinweis: Für die Steigung der Normalen und der Tangentensteigung gilt ja 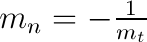
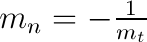
An dem Summanden mit dem höchsten Exponenten - er bestimmt das Grenzverhalten im Unendlichen.
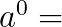 0
0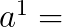 a
a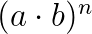 =
= 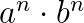
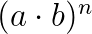 =
= 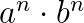
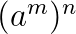 =
= 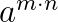
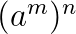 =
= 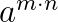
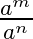 =
= 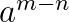
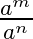 =
= 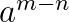
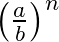 =
= 
 =
= 
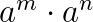 =
= 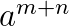
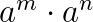 =
= 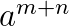
 =
= 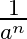
 =
=